Sep 29, 2017  Speed Coding Python - Sliding Puzzle Game motiQ Research. Unsubscribe from motiQ Research? Cancel Unsubscribe. Subscribe Subscribed Unsubscribe 10K. As introduced above, 2048 is a tile-sliding puzzle game where the objective is to maximize your score. To do so you are provided with a skeleton code in the file game.py. The following are the provided files in python: tests.py.

The Game Setup In this chapter we'll look at a one-person game that was popular in my childhood. It's a bit like the Rubic cube which came later and which is more challenging. Here is a picture of one. The game has a small platform with generally 16 slots in a 4 by 4 square. There are 15 tiles usually numbered from 1 to 15, one per slot. This leaves an empty slot.

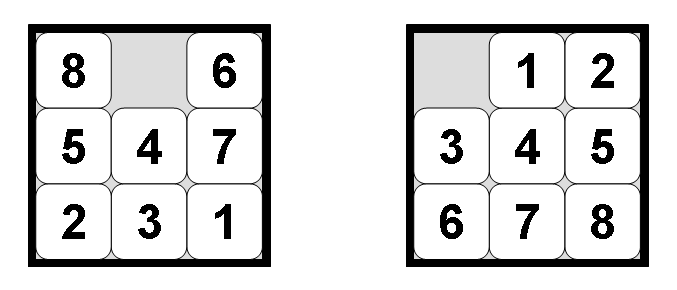
Any tile adjacent to the empty slot may slide into it, which then makes the tiles previous slot empty. The object is to slide tiles, one at a time, to bring them into order. The order is first by row and then by column, with the empty slot at the end. You can download this To keep things simple we'll first work with a 3x3 game with tiles numbered 1 to 8. Here is an example of a game in its final (solved) configuration.

1 2 3 4 5 6 7 8. The Representation of a Board configuration As we'll see, during the search for a solution many thousands of partial solutions may be floating around in our workspace. It's important to keep these partials as tight as we can. A simple string can do this nicely.

These two examples show how both a 3x3 (three by three) board and a more standard 4x4 board might look. 42_75678_9cfdbae Every configuration string is either 9 (3^2) or 16 (4^2) characters long. Each digit is uniquely present and the underscore is used to indicate the empty slot.

The string is simply ordered by row and then by column. The two goal solutions are 12345678_ and 123456789abcdef_. To have enough characters we just switched to hexidecimal. Mnf games zip file password protect. The Search for the solution This game can be played in a similar manner to the water buckets problem where we used either a stack or a queue to control a depth first or breadth first search. To avoid having to repeat this material, please first read if this material is new to you and then return.

Finding compatible USB drives is a hit and miss process. Usb xtaf xplorer xbox 360. Now you just need a USB drive that is compatible with Original Xbox.

What makes this game more interesting than water buckets is that the search space, even for the 3x3 version of the puzzle contains enough possibilites that we need be more clever in our approach. The number of possible node configurations in the 3x3 puzzle is 9 factorial or 362880. For a 4x4 puzzle the number is 8000. We'll look at doing the two brute force searches and then optimize them with 2 interesting algorithms that will greatly trim the work required.

These are the Greedy and the A-star algorithms both of which use a heuristic to estimate the 'goodness' of any particular configuration. Representing Game Nodes There is more information that must accompany the layout of the tiles. I want to take the approach of keeping this information in a tuple rather than creating an object class for the game nodes. One reason is for speed and size. Another is that by ordering the items in the tuple we will automatically get a very simple insertion into a priority queue.

Each tuple representing a game node will have the following 4 items in the order shown. • The expected cost with both past moves and estimate of future moves • The number of this past moves so far • The 9 or 16 character configuration of the board (discussed above) • A pointer to the parent node of this node or None for the start node The ordering of the information in the tuple is very important.

If you sort a set of node tuples, the order you get is by 'least expected cost'. Adding Heuristic to Solution Search In the water bucket problem, we used brute force to search for a solution. The breadth first search lets us examine and keep possible partial solutions even handily. As each new step in a partial solution was taken, the result was sent to back of the queue to let other partial solutions have their chance. In this way, the shortest and best solution to the problem is found first. A depth first approach, on the other hand, would requeue the result at the front.

This makes us hammer away at whatever we started and even if we do find a solution, it is unlikely to be the optimal one. But supposing we do something between these extremes. If we can estimate how 'good' a partial solution this, that is, how close it is to the final solution, and requeue it based on this, we can shorten the search greatly. This is the heart of the A-star algorithm.